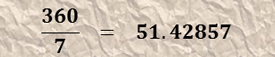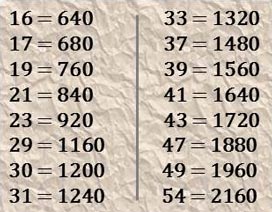The divide head and rotary table are a device used to rotate the work piece around a third machine axis, this is usually referred to as the 'C' axis and is commonly used on milling machines or borers to provide the ability to easily create accurate single or multiple machining operations around a component.
A typical use would be to quickly machine a hexagon profile around a diameter, or to produce a series of cut-outs at a specific pitch from one another. The divide head is similar to that of mounting a lathe head on a milling machine table to produce a horizontal rotating axis, where as a rotary table is more commonly used to rotate the work piece vertically. Of course both devices may be mounted then moved in multiple orientations besides that mentioned above in order to produce the profile required.
Movement of the device is a simple matter of rotating a handle in the desired direction until the degree of movement is obtained that you need to rotate the part. In simple use, the engineer would mark-off the work piece prior to mounting onto the 'C' axis, then having mounted a centre drill or pointer into the machine chuck - rotate the part until the markings align central to the spindle. Of course this method is only as accurate as ones marking-off and sight allows! Some cheaper devices are fitted with only a graduated dial for rotational movement, but for perfect precision the machinist must make use of the 'Hole Plate', which is an integral part of most 'older' or better quality dividing heads and rotary tables.